research

My overall research interests include understanding the mechanical and dynamic properties of soft and biological materials from biopolymer networks to whole tissues. I use coarse-grained models and theoretical frameworks to discover the most important parameters in these complex systems. Biopolymer networks such as collagen are constantly under both external and internal stresses. A common feature in the mechanical response of such natural biopolymer materials is that they become stronger as they are deformed. Recent studies have shown that these fiber networks undergo a mechanical phase transition from a soft to a rigid state under nonlinear deformations. Understanding this critical transition helps us to provide a productive theory for real biopolymer networks.

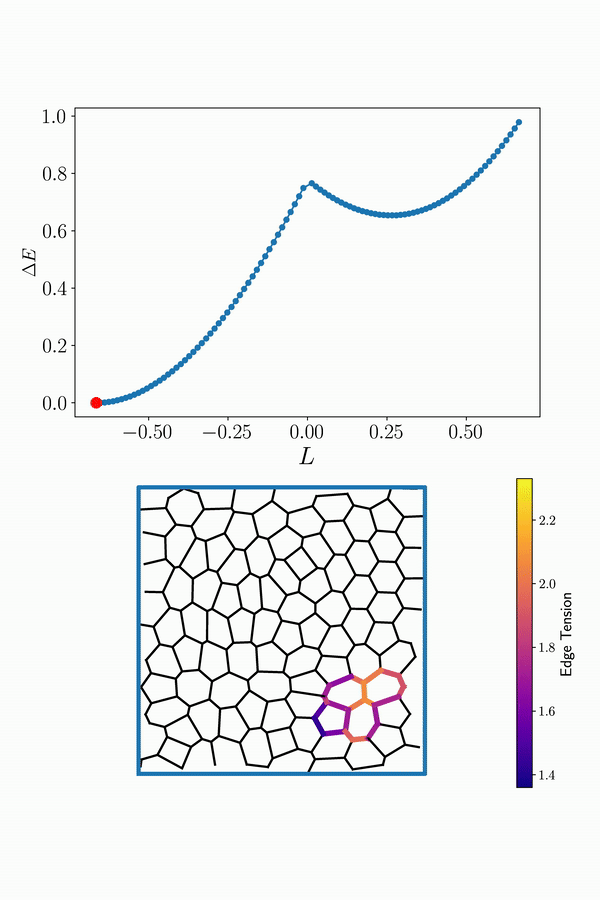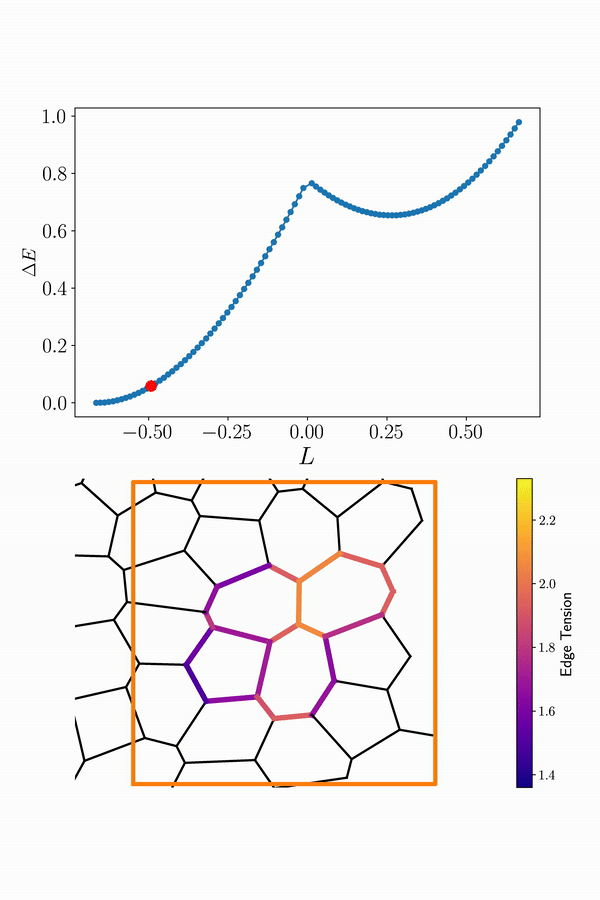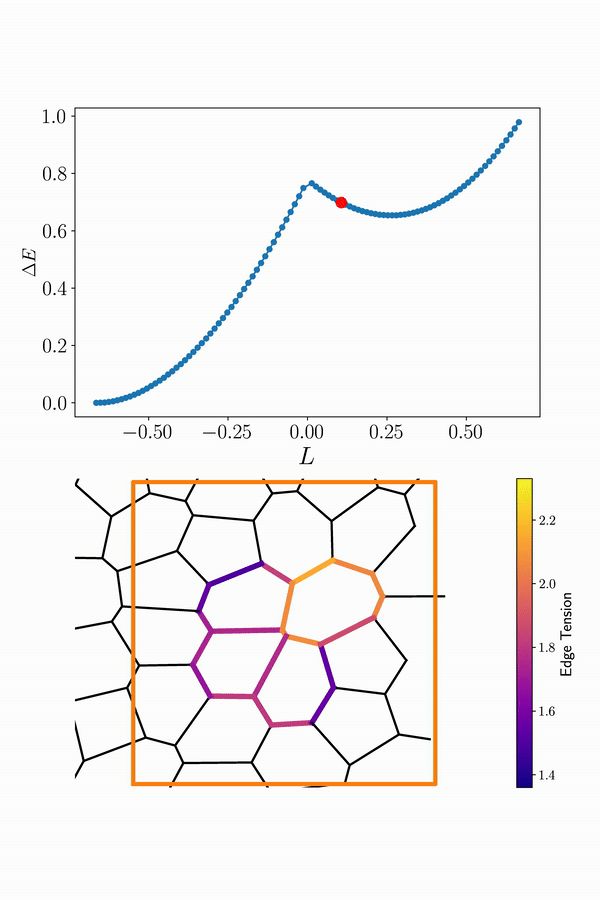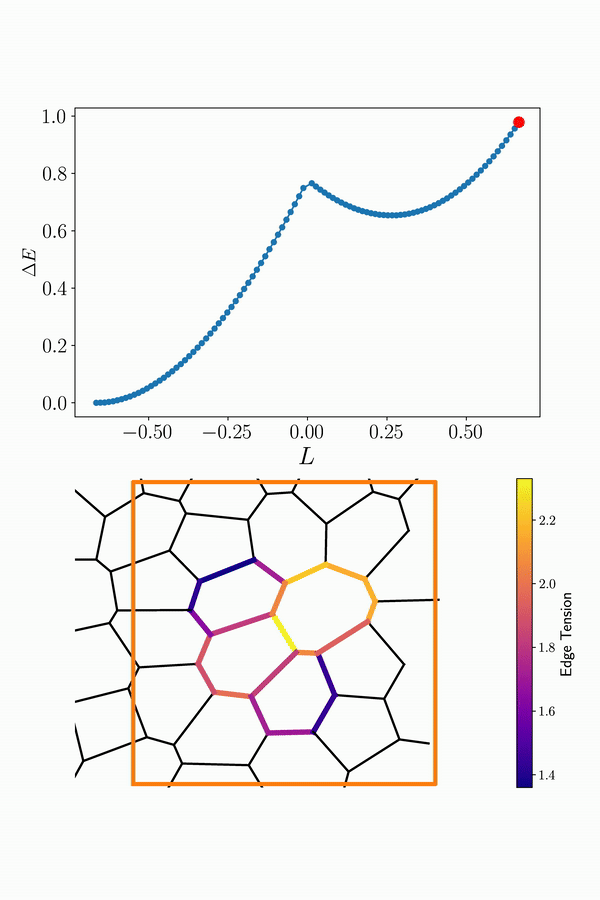
Interestingly, on the multicellular scale, it has also been shown that the behavior of tissues can be explained in terms of a transition from a solid-like to a fluid-like state based on their cellular geometry and motility. Understanding collective cell movements is important to decipher complex biological processes such as embryonic development, cancer progression, and wound healing.

A diluted triangular network with z=3.3 under a simple shear deformation. The differential shear modulus K becomes finite at a critical strain. The color bar shows the relative force on bonds. The bonds are modeled as Hookean springs.

Linear shear modulus versus the target shape index in a vertex model. The edge tensions are shown in red with a thickness proportional to their tension. As we increase the target shape index, the tissue exhibits a transition from a solid-like to a fluid-like state.

The energy barrier of T1 transitions in biological tissues. The solid-like tissues exhibit a finite energy barrier. For fluid-like states, this barrier vanishes.