publications
2025
-
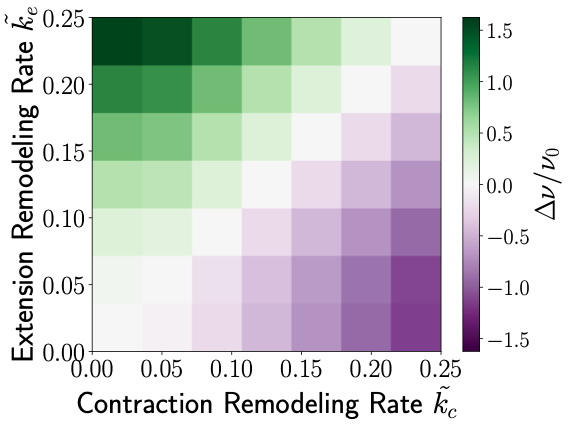 Learning Epithelial Elasticity via Local Tension RemodelingArzash, Sadjad, and Banerjee, ShiladityabioRxiv Dec 2025
Learning Epithelial Elasticity via Local Tension RemodelingArzash, Sadjad, and Banerjee, ShiladityabioRxiv Dec 2025Biological materials, like epithelial tissues, exhibit remarkable adaptability to mechanical stresses, dynamically remodeling their structure in response to external and internal forces. A key challenge is understanding how these tissues store a memory of past mechanical stimuli. Here, we investigate this memory using an active Vertex Model of epithelial sheets incorporating a local, mechanosensitive tension-remodeling rule where junctional tension updates depend on strain, acting as a slow, history-dependent variable. We demonstrate three hallmark mechanical consequences of this memory mechanism. First, a localized, short contractile cue permanently reprograms the global shear modulus, with the direction of change (stiffening or softening) controlled by the tension remodeling rate. Second, the tissue stores a long-range mechanical memory: a prior stimulus at one site modulates the tissue’s response to a subsequent, distant stimulus, mediated by coupling across the entire junctional network. Finally, we show that simple cyclic bulk deformation acts as a training protocol that autonomously tunes the tissue’s constitutive properties, including programming the Poisson ratio to auxetic (negative) values. These findings position epithelial mechanics within the framework of unsupervised physical learning, identifying the mechanosensitive remodeling rates as powerful control parameters for designing programmable tissue-scale rheology.
-
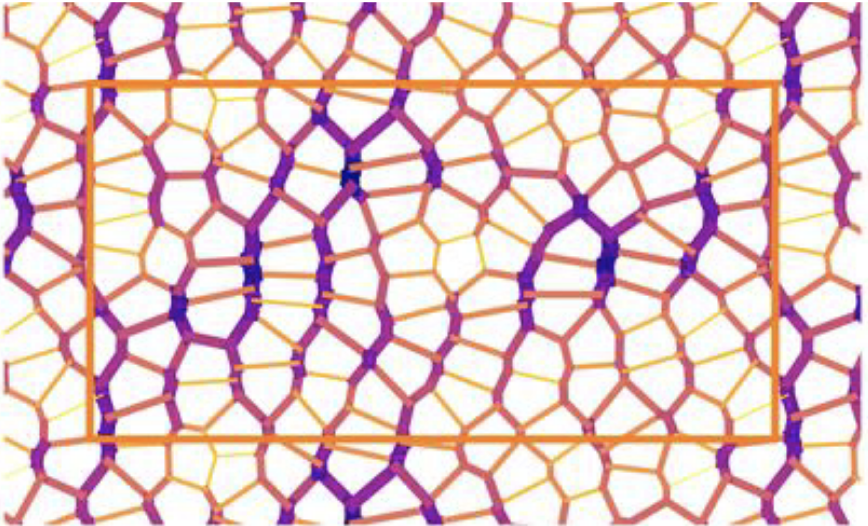 Epithelial convergent extension as a tuning processArzash, Sadjad, Liu, Andrea J., and Manning, M. LisabioRxiv Nov 2025
Epithelial convergent extension as a tuning processArzash, Sadjad, Liu, Andrea J., and Manning, M. LisabioRxiv Nov 2025Self-tuning, the ability of disordered systems to develop desired collective behaviors by tuning internal couplings in response to feedback, has recently emerged as a powerful framework for understanding adaptation in amorphous solids, mechanical metamaterials, and electrical networks. These systems can learn desired responses, encode memory, and robustly reorganize under repeated stimuli, much like artificial neural networks but without requiring processors to adjust their weights. Here, we extend this paradigm to morphogenesis and show that the epithelium can be viewed as tunable matter and that epithelial convergent extension (CE) can be understood as a self-tuning process. Using a vertex model with active interfacial tensions, we systematically compare distinct tension-update strategies, including externally imposed shear, global gradient descent optimization, and decentralized local feedback rules. We find that while all methods can generate tissue elongation, only local orientation- and length-sensitive rules reproduce key experimental features of CE, such as supracellular actomyosin pattern formation, cell shape changes, and junctional alignment. In contrast, global optimization produces homogeneous tension patterns and mechanically fragile states. By interpreting CE through the lens of tuning, our framework bridges the physics of tunable matter with developmental biology, revealing how simple, local rules enable tissues to efficiently orchestrate complex morphogenetic outcomes through decentralized mechanical adaptation.
-
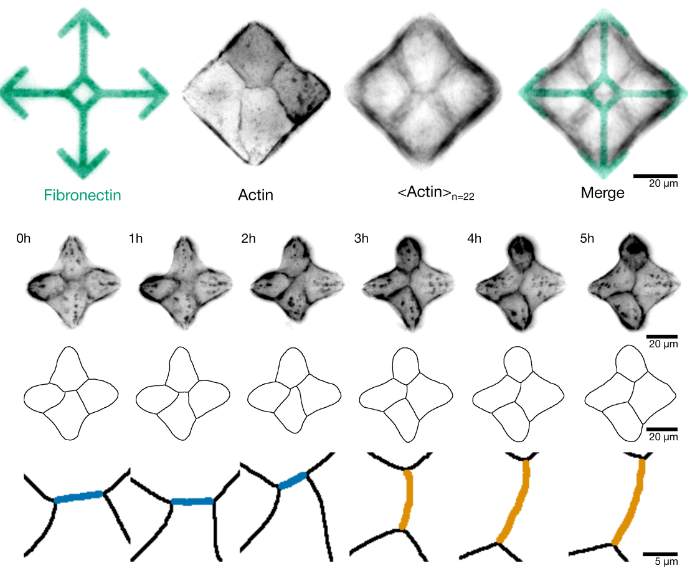 Morphogenesis-on-chip: A minimal in vitro assay for cell intercalation highlights the importance of interfacial tension and migratory forcesRuppel, Artur, Misiak, Vladimir, Arzash, Sadjad, Herrador, Daniel Selma, Cappello, Giovanni, Boudou, Thomas, Manning, Lisa, Fagotto, François, and Balland, MartialbioRxiv Jul 2025
Morphogenesis-on-chip: A minimal in vitro assay for cell intercalation highlights the importance of interfacial tension and migratory forcesRuppel, Artur, Misiak, Vladimir, Arzash, Sadjad, Herrador, Daniel Selma, Cappello, Giovanni, Boudou, Thomas, Manning, Lisa, Fagotto, François, and Balland, MartialbioRxiv Jul 2025Cell intercalation, the dynamic exchange of cellular neighbors, is fundamental to embryonic morphogenesis, tissue homeostasis, and wound healing. Despite extensive study in complex tissues, the minimal mechanical requirements driving intercalation remain poorly understood due to confounding tissue level interactions. Here, we present a novel morphogenesis-on-chip assay utilizing micropatterned cell quadruplets. This system isolates the elementary unit of intercalation while enabling quantitative force and shape measurements. Cross-shaped micropatterns generate stable four cell configurations in MDCK epithelial cells. Surprisingly, these cells spontaneously undergo T1 transitions autonomously. We combined live imaging with force inference and traction force microscopy, which revealed that intercalation emerges from two distinct mechanisms: interfacial tension dynamics and differential cell migration. Specifically, we show a correlation between central junction shrinkage and increased relative tension. Similarly, we show a correlation between central junction shrinkage and migratory forces. We successfully adapted the assay to Xenopus mesoderm cells, revealing conserved mechanical principles across cell types. Furthermore, experimentally derived effective energy landscapes closely match theoretical vertex model predictions, and suggest a dominant role for migratory forces in driving intercalation. This confirms that our minimal system recapitulates the fundamental physics of intercalation. This approach provides the first quantitative framework for studying intercalation mechanics in isolation and establishes a versatile platform for investigating morphogenetic processes. Download figureOpen in new tab
-
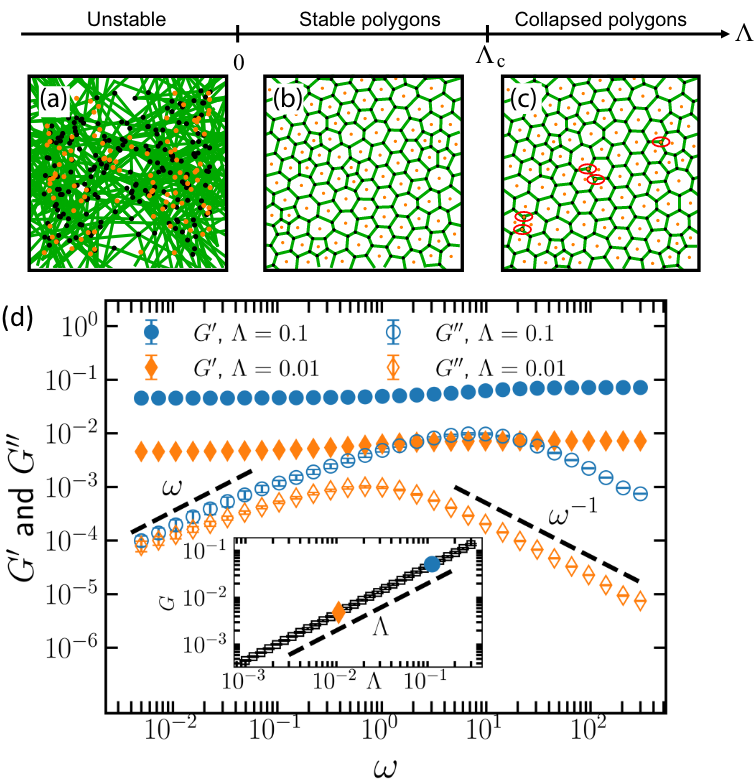 Universality in the Mechanical Behavior of Vertex Models for Biological TissuesDamavandi, Ojan Khatib*, Arzash, Sadjad*, Lawson-Keister, Elizabeth, and Manning, M. LisaPRX Life Jul 2025
Universality in the Mechanical Behavior of Vertex Models for Biological TissuesDamavandi, Ojan Khatib*, Arzash, Sadjad*, Lawson-Keister, Elizabeth, and Manning, M. LisaPRX Life Jul 2025Simple vertex models, where the cell shape is defined as a network of edges and vertices, have made useful predictions about the collective behavior of confluent biological tissues, including rigidity transitions. Quite a few different versions of vertex models have appeared in the literature, and they propose substantial differences in how the mechanical energy depends on vertex positions, yet all seem to make correct predictions. To understand how this is possible, we search for universality in the emergent mechanical behavior-including the shear modulus defined in the limit of zero-strain rate and the viscoelastic response at finite strain rates-of six different vertex models. We identify a class of models with a well-defined shear modulus, and demonstrate that these models all exhibit a crossover from a soft or floppy regime to a stiff regime. We find that the observed cell shape index (the ratio of the cell perimeter to the square root of the cell area) is a good observable order parameter for the crossover, even though the input model parameter that controls the crossover is different in each model. We also find that the finite-strain-rate viscoelastic response of all models exhibits a universal scaling with frequency, following the Zener model in the rigid phase and Burgers model in the fluid phase. The observation that a geometric observable like cell shape governs the transition, rather than a topological observable such as coordination number, suggests that second-order rigidity may be a good framework for explaining this universality. It generates an empirical prediction that a broad class of vertex models with second-order rigidity transitions should also exhibit these universal mechanical features, and helps to explain why many different vertex models are able to robustly predict these features in experiments.
-
 Rigidity of epithelial tissues as a double optimization problemArzash, Sadjad, Tah, Indrajit, Liu, Andrea J., and Manning, M. LisaPhysical Review Research Feb 2025
Rigidity of epithelial tissues as a double optimization problemArzash, Sadjad, Tah, Indrajit, Liu, Andrea J., and Manning, M. LisaPhysical Review Research Feb 2025How do cells tune emergent properties at the scale of tissues? One class of such emergent behaviors are rigidity transitions, in which a tissue changes from a solidlike to a fluidlike state or vice versa. Here we introduce a way for a tissue described by a vertex model to tune its rigidity by using �tunable degrees of freedom.� We use the vertex model elastic energy as a cost function and the cell stiffnesses, target shapes, and target areas as different sets of degrees of freedom describing cell-cell interactions that can be tuned to minimize the cost function. We show that the rigidity transition is unaffected when cell stiffnesses are treated as tunable degrees of freedom. When preferred shapes or areas are treated as tunable degrees of freedom, however, induced spatial correlations in target cell shapes or areas shift the rigidity transition. These observations suggest that tissues can coordinate changes in cell-scale properties, treated here as tunable degrees of freedom, to achieve desired tissue-scale behaviors.
2024
-
 Effects of local incompressibility on the rheology of composite biopolymer networksGannavarapu, Anupama, Arzash, Sadjad, Muntz, Iain, Shivers, Jordan L., Klianeva, Anna-Maria, Koenderink, Gijsje H., and MacKintosh, Fred C.The European Physical Journal E May 2024
Effects of local incompressibility on the rheology of composite biopolymer networksGannavarapu, Anupama, Arzash, Sadjad, Muntz, Iain, Shivers, Jordan L., Klianeva, Anna-Maria, Koenderink, Gijsje H., and MacKintosh, Fred C.The European Physical Journal E May 2024Fibrous networks such as collagen are common in biological systems. Recent theoretical and experimental efforts have shed light on the mechanics of single component networks. Most real biopolymer networks, however, are composites made of elements with different rigidity. For instance, the extracellular matrix in mammalian tissues consists of stiff collagen fibers in a background matrix of flexible polymers such as hyaluronic acid (HA). The interplay between different biopolymer components in such composite networks remains unclear. In this work, we use 2D coarse-grained models to study the nonlinear strain-stiffening behavior of composites. We introduce a local volume constraint to model the incompressibility of HA. We also perform rheology experiments on composites of collagen with HA. Theoretically and experimentally, we demonstrate that the linear shear modulus of composite networks can be increased by approximately an order of magnitude above the corresponding moduli of the pure components. Our model shows that this synergistic effect can be understood in terms of the local incompressibility of HA, which acts to suppress density fluctuations of the collagen matrix with which it is entangled.
2023
-
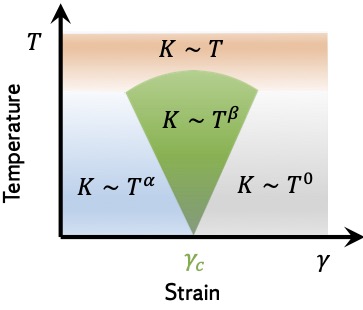 Mechanical criticality of fiber networks at a finite temperatureArzash, Sadjad, Gannavarapu, Anupama, and MacKintosh, Fred C.Physical Review E Nov 2023
Mechanical criticality of fiber networks at a finite temperatureArzash, Sadjad, Gannavarapu, Anupama, and MacKintosh, Fred C.Physical Review E Nov 2023At zero temperature, spring networks with connectivity below Maxwell’s isostatic threshold undergo a mechanical phase transition from a floppy state at small strains to a rigid state for applied shear strain above a critical strain threshold. Disordered networks in the floppy mechanical regime can be stabilized by entropic effects at finite temperature. We develop a scaling theory for this mechanical phase transition at finite temperature, yielding relationships between various scaling exponents. Using Monte Carlo simulations, we verify these scaling relations and identify anomalous entropic elasticity with sublinear 𝑇 dependence in the linear elastic regime. While our results are consistent with prior studies of phase behavior near the isostatic point, the present work also makes predictions relevant to the broad class of disordered thermal semiflexible polymer networks for which the connectivity generally lies far below the isostatic threshold.
2022
-
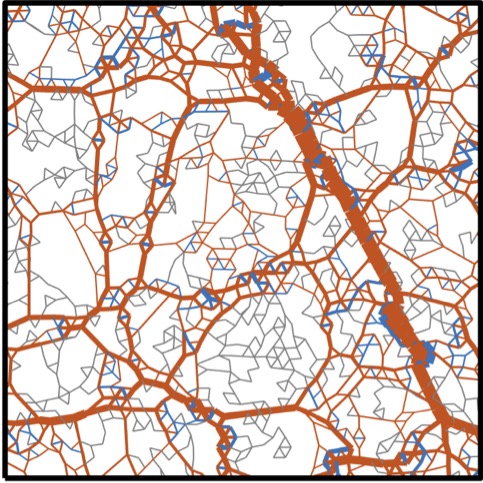 Mechanics of fiber networks under a bulk strainArzash, Sadjad, Sharma, Abhinav, and MacKintosh, Fred C.Physical Review E Dec 2022
Mechanics of fiber networks under a bulk strainArzash, Sadjad, Sharma, Abhinav, and MacKintosh, Fred C.Physical Review E Dec 2022Biopolymer networks are common in biological systems from the cytoskeleton of individual cells to collagen in the extracellular matrix. The mechanics of these systems under applied strain can be explained in some cases by a phase transition from soft to rigid states. For collagen networks, it has been shown that this transition is critical in nature and it is predicted to exhibit diverging fluctuations near a critical strain that depends on the network’s connectivity and structure. Whereas prior work focused mostly on shear deformation that is more accessible experimentally, here we study the mechanics of such networks under an applied bulk or isotropic extension. We confirm that the bulk modulus of subisostatic fiber networks exhibits similar critical behavior as a function of bulk strain. We find different nonmean-field exponents for bulk as opposed to shear. We also confirm a similar hyperscaling relation to what was previously found for shear.
2021
-
 Shear-induced phase transition and critical exponents in three-dimensional fiber networksArzash, Sadjad, Shivers, Jordan L., and MacKintosh, Fred C.Physical Review E Aug 2021
Shear-induced phase transition and critical exponents in three-dimensional fiber networksArzash, Sadjad, Shivers, Jordan L., and MacKintosh, Fred C.Physical Review E Aug 2021When subject to applied strain, fiber networks exhibit nonlinear elastic stiffening. Recent theory and experiments have shown that this phenomenon is controlled by an underlying mechanical phase transition that is critical in nature. Growing simulation evidence points to non-mean-field behavior for this transition and a hyperscaling relation has been proposed to relate the corresponding critical exponents. Here, we report simulations on two distinct network structures in three dimensions. By performing a finite-size scaling analysis, we test hyperscaling and identify various critical exponents. From the apparent validity of hyperscaling, as well as the non-mean-field exponents we observe, our results suggest that the upper critical dimension for the strain-controlled phase transition is above three, in contrast to the jamming transition that represents another athermal, mechanical phase transition.
2020
-
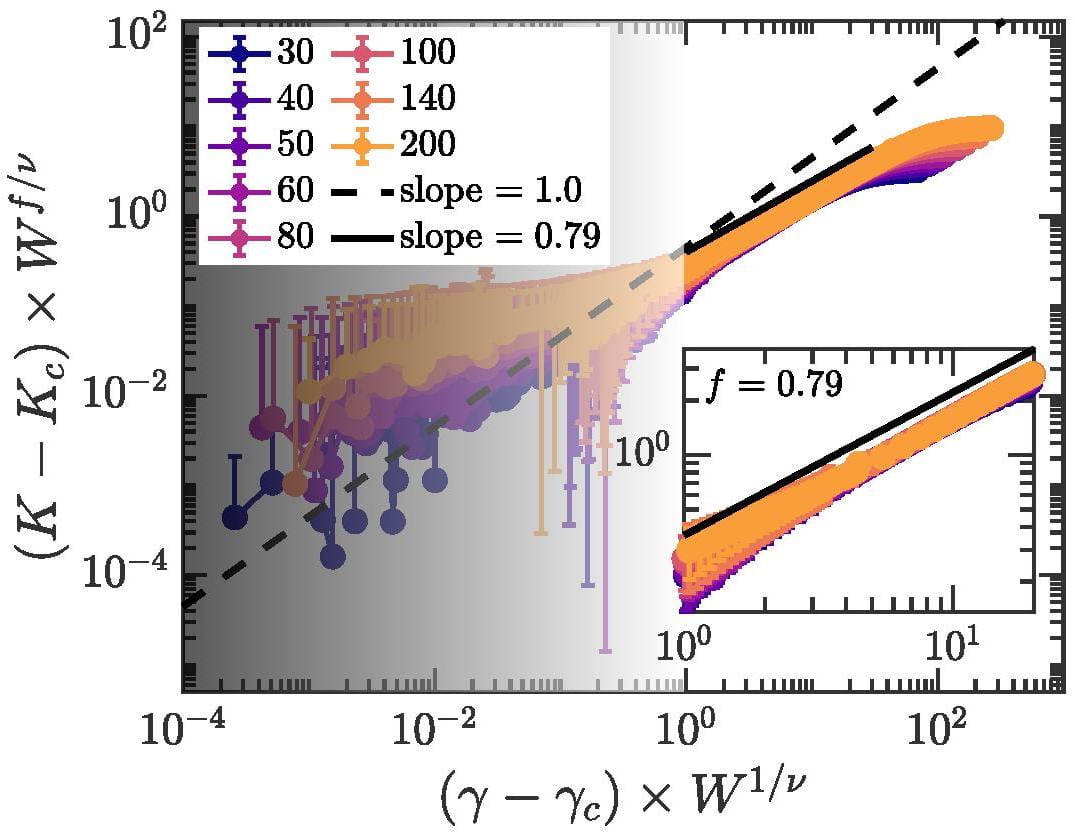 Finite size effects in critical fiber networksArzash, Sadjad, Shivers, Jordan L., and MacKintosh, Fred C.Soft Matter Jul 2020
Finite size effects in critical fiber networksArzash, Sadjad, Shivers, Jordan L., and MacKintosh, Fred C.Soft Matter Jul 2020Fibrous networks such as collagen are common in physiological systems. One important function of these networks is to provide mechanical stability for cells and tissues. At physiological levels of connectivity, such networks would be mechanically unstable with only central-force interactions. While networks can be stabilized by bending interactions, it has also been shown that they exhibit a critical transition from floppy to rigid as a function of applied strain. Beyond a certain strain threshold, it is predicted that underconstrained networks with only central-force interactions exhibit a discontinuity in the shear modulus. We study the finite-size scaling behavior of this transition and identify both the mechanical discontinuity and critical exponents in the thermodynamic limit. We find both non-mean-field behavior and evidence for a hyperscaling relation for the critical exponents, for which the network stiffness is analogous to the heat capacity for thermal phase transitions. Further evidence for this is also found in the self-averaging properties of fiber networks.
-
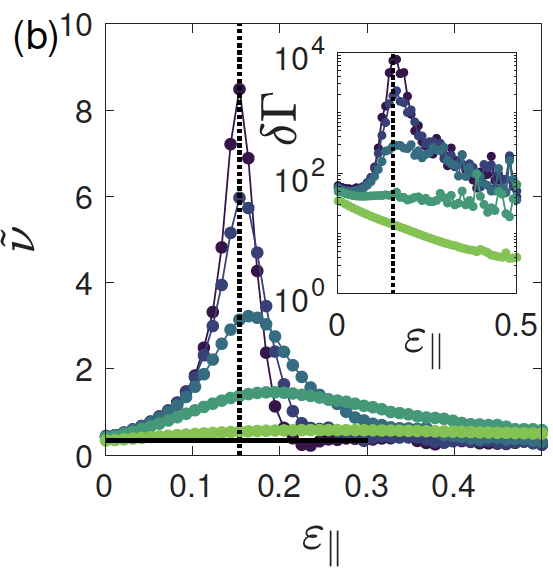 Nonlinear Poisson Effect Governed by a Mechanical Critical TransitionShivers, Jordan L., Arzash, Sadjad, and MacKintosh, F. C.Physical Review Letters Jan 2020
Nonlinear Poisson Effect Governed by a Mechanical Critical TransitionShivers, Jordan L., Arzash, Sadjad, and MacKintosh, F. C.Physical Review Letters Jan 2020Under extensional strain, fiber networks can exhibit an anomalously large and nonlinear Poisson effect accompanied by a dramatic transverse contraction and volume reduction for applied strains as small as a few percent. We demonstrate that this phenomenon is controlled by a collective mechanical phase transition that occurs at a critical uniaxial strain that depends on network connectivity. This transition is punctuated by an anomalous peak in the apparent Poisson’s ratio and other critical signatures such as diverging nonaffine strain fluctuations.
2019
-
 Scaling Theory for Mechanical Critical Behavior in Fiber NetworksShivers, Jordan L., Arzash, Sadjad, Sharma, Abhinav, and MacKintosh, Fred C.Physical Review Letters May 2019
Scaling Theory for Mechanical Critical Behavior in Fiber NetworksShivers, Jordan L., Arzash, Sadjad, Sharma, Abhinav, and MacKintosh, Fred C.Physical Review Letters May 2019As a function of connectivity, spring networks exhibit a critical transition between floppy and rigid phases at an isostatic threshold. For connectivity below this threshold, fiber networks were recently shown theoretically to exhibit a rigidity transition with corresponding critical signatures as a function of strain. Experimental collagen networks were also shown to be consistent with these predictions. We develop a scaling theory for this strain-controlled transition. Using a real-space renormalization approach, we determine relations between the critical exponents governing the transition, which we verify for the strain-controlled transition using numerical simulations of both triangular lattice-based and packing-derived fiber networks.
-
 Stress relaxation in F-actin solutions by severingArzash, Sadjad, McCall, Patrick M., Feng, Jingchen, Gardel, Margaret L., and MacKintosh, Fred C.Soft Matter Aug 2019
Stress relaxation in F-actin solutions by severingArzash, Sadjad, McCall, Patrick M., Feng, Jingchen, Gardel, Margaret L., and MacKintosh, Fred C.Soft Matter Aug 2019Networks of filamentous actin (F-actin) are important for the mechanics of most animal cells. These cytoskeletal networks are highly dynamic, with a variety of actin-associated proteins that control cross-linking, polymerization and force generation in the cytoskeleton. Inspired by recent rheological experiments on reconstituted solutions of dynamic actin filaments, we report a theoretical model that describes stress relaxation behavior of these solutions in the presence of severing proteins. We show that depending on the kinetic rates of assembly, disassembly, and severing, one can observe both length-dependent and length-independent relaxation behavior.
-
 Stress-stabilized subisostatic fiber networks in a ropelike limitArzash, Sadjad, Shivers, Jordan L., Licup, Albert J., Sharma, Abhinav, and MacKintosh, Fred C.Physical Review E Apr 2019
Stress-stabilized subisostatic fiber networks in a ropelike limitArzash, Sadjad, Shivers, Jordan L., Licup, Albert J., Sharma, Abhinav, and MacKintosh, Fred C.Physical Review E Apr 2019The mechanics of disordered fibrous networks such as those that make up the extracellular matrix are strongly dependent on the local connectivity or coordination number. For biopolymer networks this coordination number is typically between 3 and 4. Such networks are sub-isostatic and linearly unstable to deformation with only central force interactions, but exhibit a mechanical phase transition between floppy and rigid states under strain. The introduction of weak bending interactions stabilizes these networks and suppresses the critical signatures of this transition. We show that applying external stress can also stabilize subisostatic networks with only tensile central force interactions, i.e., a ropelike potential. Moreover, we find that the linear shear modulus shows a power-law scaling with the external normal stress, with a non-mean-field exponent. For networks with finite bending rigidity, we find that the critical stain shifts to lower values under prestress.